칼만필터(Kalman Filter) – 뿡뿡너구리의 블로그

출처 : http://msnayana.blog.me/80106682874

루프만 칼만이 1960년대초 개발한 필터로

컴퓨터비젼,로봇, 로켓, 위성, 미사일, 제어분야에 많이 이용되는 알고리즘인데

이것을 GPS,주식, 날씨예측, 인구예측같은 부분에도 이용을 하고 있다~~ 미래를 위해 좀 정리해보자^^..

칼만필터는

과거의 측정데이타(기존에 알고있던것)와 새로운 측정데이타를 사용하여 데이터에 포함된 노이즈를 제거시켜

새로운 결과를 추정(estmate)하는데 사용하는 알고리즘으로 선형적움직임을 가지는 대상을 재귀적적용으로 동작시킨다.

칼만필터는 1960년대에 아폴로 우주선의 달 여행시에 처음 적용되었다는데 현재는 다양한 종류의 칼만필터가 개발되어 있다.

Schmidt 의 extended filter, information filter, Bierman 과 Thornton 등등에 의해 개발된 다양한 squrar-root filter 들이 있다고 한다.

여기서 필터는

정수기의 필터처름 무엇을 걸러내는 역활로서, 측정데이타에 포함된 불확실성(noise)을 필터링하는 것으로

대상으로부터 얻을 수 있는 데이타가 완벽할수 없기에 부족한 성질을 보충한다고 보면 될 것 같다.

즉, 측정데이타나 신호가 잡음을 동반하는데 여기서 원하는 신호나 정보를 골라내는 알고리즘이라고 보면 된다.

확률에 기반한 예측시스템이므로 이것의 대상은 정규분포(가우시안분포)를 가지는 대상이 된다.

정규분포는 여기서 참조 하시고 : http://blog.naver.com/msnayana/80107833229

실제 데모뷰예 : http://www.youtube.com/watch?v=0GSIKwfkFCA&feature=related

추정 이론은 통계학과 신호처리의 한 분야이며,

측정 또는 관찰된 자료에 기반하여 모수(모집단을 대표하는 값)의 값을 추정하는 것을 다룬다.

추정을 위한 방법으로는

칼만 필터,바이너 필터,마르코프 체인 몬테 카를로,베이즈 추정자,Method of moments estimators
MAP(Maximum a posteriori),MVUE(Minimum variance unbiased estimator)등이 사용된다고 한다.

서울시의 가구의 평균소득을 조사한다고 할때

전수조사를 하지 않는이상 모집단을 대표하는 값인 모수를 알수 있는 방법은 없기에 단순히 추정을 통하여 추측하게 된다.

표본(샘플)에서 구한 통계값을 전체로 확대하여 추정하는데 이때 평균이나 표준편차나 분산이 모수로 사용된다.

다시 말하면 전수조사하지 않는 이상 모수를 절대 알수 없으므로, 모수를 추정하게 되고 이런기법중에 하나가 칼만필터이다.

자연계의 움직임은 어느정도 예측이 가능하며 일반적 움직임 물성을 가지는 것이 당연하다.

누적된 과거데이타와 현재 얻을 수있는 최선의 데이타로 현상태를 추정하고자 함은 우리의 모든 현상에서 요구되는 것으로

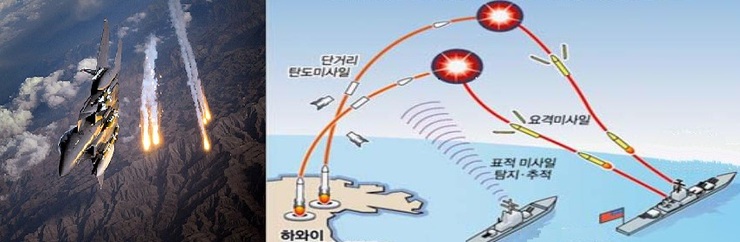
미사일이나 주식의 흐름이나 거의 같다.

실제 응용에 있어서는 시스템이 비선형이고 잡음도 Gaussian이 아닌 경우가 많으므로

칼만필터의 변형이 요구되는데 Extended Kalman Filter(EKF)가 가장 많이 사용되고 있다.

EKF 는 선형화 칼만필터(Linearized KF)와 유사하나 선형화하는 기준점을 계속 갱신해 나간다는 특징을 가지고 있다.

재귀적 자료처리의 예

처리할 자료의 양이 그리 많지 않을 때는 모든 자료를 기억해두었다가 한번에 계산하는 것이 간편하다.

하지만 엄청난 양의 자료가 계속 들어온다면 저장 장소 및 처리 시간을 고려해야 한다.

스트림처름 밀려들어 오는 데이타를 다 저장않고 현재값과 과거의 한두개 값만 기억하여

데이타 전체의 평균(모수)을 알수는 없을까?

이것은 재귀적 자료처리(recursive data processing)라는 방법으로 쉽게 처리가 가능하다고 한다.

예를들면

어떤 집단의 평균을 알고자 하는경우가 있을 수 있다.

82 + 78 + 35 + 67 + 71 + 47 + 99 + 11 + 39 + 97 = 626 /10 = 62.6

위 경우처름 10개의 값이 있을때 전부 더하여 10으로 나누면 평균이 된다.

즉 첫번값 K1에 두번째 값 K2를 더하여 2로 나누면 두번째의 평균이 됨은 무수히 하는 행동이다.

이렇게 반복하면 들어오는 모든 값을 기억해야하는 불편함이 있다.

Y(1) = K1
Y(2) = (K1+K2)/2

Y(3) = (K1+K2+K3)/3

Y(4) = (K1+K2+K3+K4)/4

Y(5) = (K1+K2+K3+K4+K5)/5
Y(n) = (K1+K2+.........+Kn)/n

좀 바꿔보면..
Y(1) = K1
Y(2) = (K1+K2)/2                 => (Y(1)*1+K2)/2
Y(3) = (K1+K2+K3)/3             => (Y(2)*2+K3)/3
Y(4) = (K1+K2+K3+K4)/4        => (Y(3)*3+K4)/4

Y(5) = (K1+K2+K3+K4+K5)/5 => (Y(4)*4+K5)/5
:
Y(n) = (K1+K2+.........+Kn)/n => (Y(n-1)*(n-1)+Kn)/n

위 식의 바뀐일반식에서 Y(n) = Y(n-1) * ((n-1)/n) + (1/n)*Kn 이렇게도 치환된다.

이식의 장점은

계속 들어오는(혹은 지나간) 각각의 값들을 모두 기억해 둘 필요가 없다는 것.
즉 n번째 평균을 구할 때 Y(n-1)와 지금 n번째라는 두개의 값만 가지고 있다면

문제없이 현재인 n번째의 평균을 구할 수 있게되는 간편함을 제공한다.

위의 식에서

Y(2) = (K1+K2)/2 라고 한것은 두개를 합해서 2로 나눠서 처리했기에 K1과 K2는 중요도가 꼭 같다.

하지만 K1이 더 가치있고 K2가 엄청 가치가 적다거나 뭔가 믿을수가 없는 데이타라면 데이타의 중요도를 줄여야 한다.

즉

Y(2) = (K1+K2)/2 ===> Y(2) = ( K1*1.0 + K2*0.5 )/2 이렇게 말이다.

이것은 일반식이 아니며 데이타의 중요도는 표준편차로 표현이 가능하다.

표준편차는 그 데이타가 평균에서 얼마나 벗어나 있는가를 나타내는 지표인데 나홀로 데이타이면 중요도가 별로이다.

각 데이타의 중요도는 표준편차 제곱에 반비례한다고 알려져 있는데

표준편차가 크면 클수록 그 값의 중요도는 떨어지며 평균에 대한 기여도가 적어지게 된다.

이렇게하여

연속적 입력데이타를 데이타의 중요도를 감안하여 과거와 현재의 두개데이타로 평균을 구할수 있게 되었다.

이전의 출력값과 새로운 입력값을 이용하여

새로운 최적값 (optimized state variables) 을 계산하는 측정갱신 알고리즘(measurement update algorithm)의 스칼라 형태가 만들어 지는데 칼만필터의 기본식은 일반적으로 행렬 또는 벡터형태로 사용되고 있다.

최적추정값 = 재귀적자료처리 + 데이타의 중요도(표준편차) + ?

칼만 필터의 기본개념은

과거와 현재값을 가지고 재귀적(recursive)연산(data processing)을 통하여 최적 (optimal) 값을 추적하는 것이다.

스칼라 칼만필터 : http://www.swarthmore.edu/NatSci/echeeve1/Ref/Kalman/ScalarKalman.html

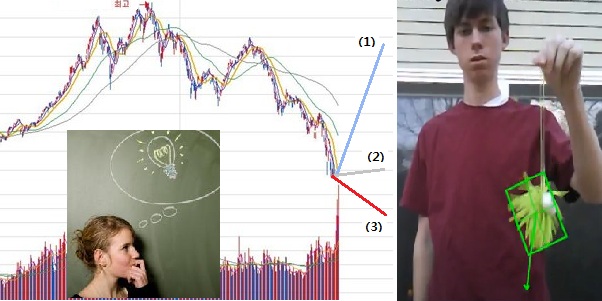
구름에 가려진 비행체를 추적하는 미사일이 비행체의 방향을 추정하는 것이나

빠른게 변하는 금리나 주식의 흐름을 예측(추정)하는 것이나 모두 현재가 아닌 바로 다음순간을 현재와 과거데이타로 예측하는 것으로

추정은 통계적방법으로 인과관계를 기반으로 예측하는 것이다.

http://www.youtube.com/watch?v=vfgIXdbEyUw&feature=related

http://www.youtube.com/watch?v=095IOfqF4nY&feature=related

칼만 필터는

수학적으로 선형 시스템(Linear System)의 상태를 예측해서 발생할 수 있는 오류를 최소화 하면서 예측한다.

선형시스템 (Linear Systems)이라는 것은 y= ax + b 와 같은 것인데 자연의 대부분 속성은 비선형을 보인다.

사실 비선형을 위해 UKF나 EKF를 주로 사용하지만 비선형을 선형으로 단순화시킬수 있는 것은 대충 적용이 가능하다고 한다.

칼만필터를 적용하기 위해서는 신호가 선형적으로 근사화되어야 하는데... 여기에 좋은 자료가 있군요..
http://academic.csuohio.edu/simond/courses/eec644/kalman.pdf

http://www.cs.unc.edu/~tracker/media/pdf/SIGGRAPH2001_CoursePack_08.pdf

http://blog.naver.com/hangondragon/20066836673

http://blog.naver.com/hangondragon/20066898769
http://blog.naver.com/housemoon/96039559 ======== 여기에 비행기에 적용한 논문과 소스가 있네요..

흠!!

하지만 읽어보면 어렵고 머리에 그림이 그려지지 않으니..

내 나쁜 머리만 탓할 수 밖에 없네.....

결국 내가 이해하는 방법으로 내 식으로 적는 수박에.. 이건 나만을 위한 정리노트이니....

다시 한번 필터라는 말에 집중하자..

주파수 영역에서의 특성에 따라 LPF(low-pass filter), HPF(high-pass filter), BPF(band-pass filter)등으로 분류하고 신호를 선택한다.

하지만 물리적 필터가 아닌 DSP같은 계산에 의한 필터링에서는 주파수영역은 최적해를 구하는 것이 어려우므로

이것을 시간영역에서 처리하여 Winer Filter의 기술적 문제점을 완전히 해결한 것이 칼만이라고 하니...

우리가 많이 배운 퓨리에변환이나 라플라이스변환도 시간축과 주파수축의 변환이 었는데...

신호는

영상이나 음성 혹은 좌표,압력등으로 다양한데 센서를 거치면서 센서에 의한 물성적 노이즈가 첨가 되는 경우가 대부분이다.

차의 속도는 도로노면에 돌이 많거나 사람이 많아도 영향을 미치고

음성은 마그네틱의 고유잡음으로도 본래 음성에 마그네틱노이즈(히스테리시스)가 첨가되어 나타난다.

영상도 영상센서(스미어,저조도노이즈,고정잡음,모아레등)에 첨가되어 나타나므로 적절한 광학/계산필터를 추가한다.

움직임을 추적하려면 어떠한 노이즈를 필터링해야만 하는 걸까?

가만히 생각해 보면 물체는 자신의 관성에 영향을 받고 주변의 간섭적 노이즈에 영향을 받을 것 같은데...

대부분의 사람들도 오래 누적된 신용데이타를 벗어난 행위를 거의 하지 않는 것 같은 통계적 처리가 행동예측을 가능케 하는 것 처름..

선형시스템은 y=ax+b로 표현되는 정도이므로 단순하나 에러가 포함된다.

비선형을 위해 UKF나 EKF를 주로 사용하지만 비선형을 선형으로 단순화시킬수 있는 것은 대충 적용이 가능하다고 한다

칼만필터(LKF)의 알고리듬을 컴퓨터로 구현하는 단계를 살펴보자.
1) 현재의 상태변수 추정치 및 공분산 값으로 부터 다음 측정시간에서의 상태변수 추정치 및 공분산을 계산하는 단계.

수치적으로는 시간적분에 해당하는 단계이며 Propagation 단계이다.
2) 새로운 측정치와 Propagation으로 부터 얻어진 상태변수 추정치를 혼합하여 상태변수 추정치를 새롭게 계산하는 단계.

이 단계에서 칼만필터 게인 K를 최적추정 이론에 따라 계산하는데 Update 단계라 한다.

선형시스템은

직접 센서들에서 측정가능한 측정모델함수(오차포함)와

현재상태를 표현하지만 직접 측정이 불가능한 상태모델함수로 단순화시킨 두개의 식으로 표현이 가능하다고 한다.

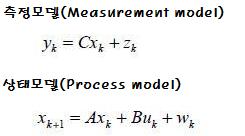
위 식에서

Y는 측정값으로 z는 측정잡음이며 상태모델의 x값을 이용하여 Y를 확정한다.

X는 시스템의 현재상태값으로 위치나 속도등이 될수 있는데 w인 프로세서잡음과 Y를 이용하여 구할수 있다.

실제 구하려는 것이 다음 시간의 X 값이다.

u라는 변수엔 시스템에서 제어 할수 없는 잡음(예로 화이트노이즈)이 들어오고

현재의 X값에 프로세서잡음 w가 합쳐져 정해지는데 결국 현재의 x가 Y와 z에 영향받으므로... 흠 피드백이 걸리네.

실제 표현식은 아래와 같다.

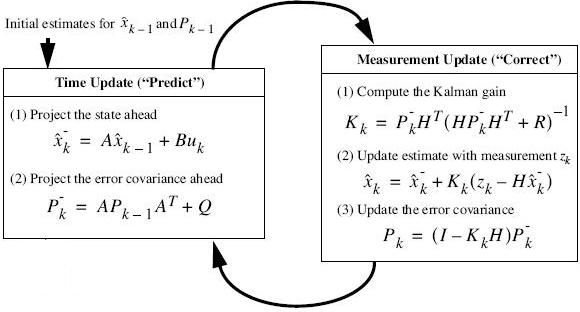
Xk-1은 이전상태이며 Xk는 현상태이다. 물론 P도 같다.

K는 칼만게인(Kalman Gain), P는 추정오차공분산 메트릭스(the estimation error corvariance matrix)

^는 상태변수라는 표현이고 x-의 -는 이전상태를 말한다고 보면 될것 같다.

Q(예측노이즈 공분산), R(측정노이즈 공분산),A,B,H,u

여기서는 Time Update와 Measurement Update라는 두개의 상태로 나눠 구현되었다.

이것은 위에서 말한 상태모델함수가 Time Update이고 측정모델함수가 Measurement Update와 같다

초기에

X와 P를 위한 초기예측이 제공되어야 한다.

상수항인 변하지 않는 행렬 A,H,Q,R 값이 있고 루틴을 시작하기에 앞서 초기값이 이미 있어야 한다.

Time Update : 예측단계(시간갱신) : 이전데이타를 근거로 예측

1) 이전상태벡터x에 A를 곱하고 u(예측오차잡음)에 B를 곱하여 구한 X는 순수한 상태예측값이다.

2) 에러보정을 위해 수행하는 단계로 수집된 자료를 기반으로 얼마의 보정을 할지 결정한다. (프로세스노이즈 예측)

Measurement Update : 교정단계(측정치갱신) : 새로운 측정값으로 교정

1) 칼만게인을 구한다.( 프로세스노이즈(예측오차분)과 측정노이즈(실측잡음분)를 이용하여 계산)

2) 측정잡음z를 추가하여 현재의 상태벡터x를 구한다.

3) 예측오류인 추정오차공분산 P를 구한다.

어떤 센서에서 측정데이타를 잡으면 노이즈(센서잡음,ADC잡음,처리잡음..)가 생기게 되고, 이것을 통상 필터로 제거시킨다.

이것을 측정노이즈라고 하는데 칼만필터에서는 측정노이즈를 가우시안 확률모델이라 칭하고 같은 의미로 사용한다.

가우시안 확률모델은 정규분포로 평균과 분산을 알면 신호특성을 완벽히 표현가능한 상태분포로

대부분의 발생노이즈도 제품의 불량처름 정규분포로 표현이 가능하기 때문이다.

또한 현재측정에는 항상 노이즈가 있어 오차를 예측하여 수정하면서 제어해야 문제가 누적되지 않는다.

예측은 항상 오차를 보이는데 이것을 Process noise라 하고

이 프로세스노이즈(예측오차분)과 측정노이즈(실측잡음분)을 공분산을 이용하여 가중치처리를 한다.

즉 Process Noise가 Measurement Noise보다 분산이 크다면 Measurement에 더 큰 가중치가 곱해질 것이며,
그 반대라면 모델을 이용한 예측 값에 더 큰 가중치가 곱해져 업데이트 되는 구조로 작동된다.

변하지 않는 행렬값과 초기값을 가지고 예측루틴의 값을 구하게 된다.

이후 이 값을 이용하여 Kalman Gain 과 측정값 Z 를 이용하여 다음 예측치를 보정하고 Process Noise 분산을 보정한다.

이런 과정을 반복하여 칼만 필터는 동작한다.

수식이 많이 어렵다.

또 위식에서 추정오차 공분산(estimation error corvariance) P를 만나서 새용어인 공분산(corvariance)을 알고가야 한다.

공분산(共分散, Covariance)은 2개의 확률변수의 상관정도를 나타내는 값이다.
만약 2개의 변수중 하나의 값이 상승하는 경향을 보일 때,
다른 값도 상승하는 경향의 상관관계에 있다면 공분산의 값은 양수가 될 것이다.
반대로 2개의 변수중 하나의 값이 상승하는 경향을 보일 때,
다른 값이 하강하는 경향을 보인다면 공분산의 값은 음수가 된다.
이렇게 공분산은 상관관계의 상승 혹은 하강하는 경향을 이해할 수 있다.