출처 : http://blog.naver.com/chogaehwan/220773857547
캬하 드디어 했다.
unscented 칼만 필터…뭐라고 설명해야 할까..?
EKF는 비선형을 예측값이나 직전값에서 선형화하여 칼만필터를 이용하였다.
하지만 UKF는 직전 추정값 근처 2n+1개의 샘플들을 추출하여 각각 가중치를 두어
추정값과 측정값을 예측한다. 각값에는 평균과 분산이 있게 된다.
그 값들로 추정치와 오차 공분산을 계산해내는 것이다.
확률 칼만 필터라고 보면 오히려 이해가 가기 쉬울 것 같다. unscented가 뭐야 …stochastic kalman filter가 낫지…
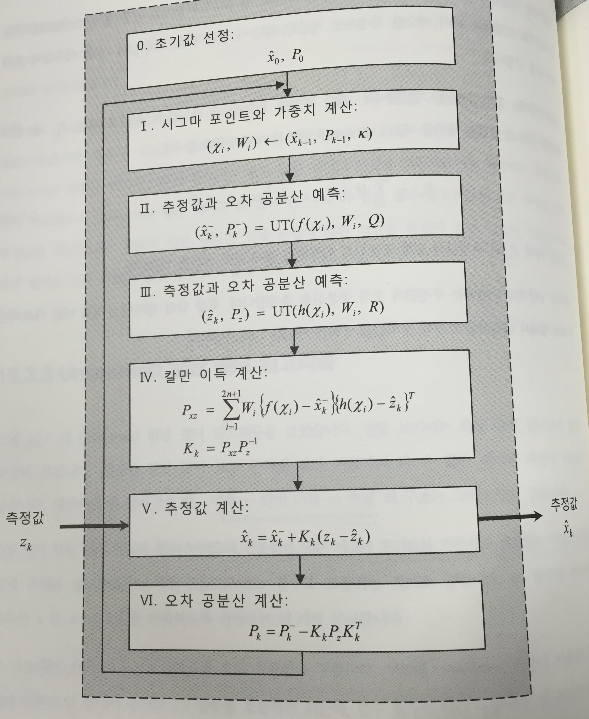
하튼 기본 구조는 아래와 같다.
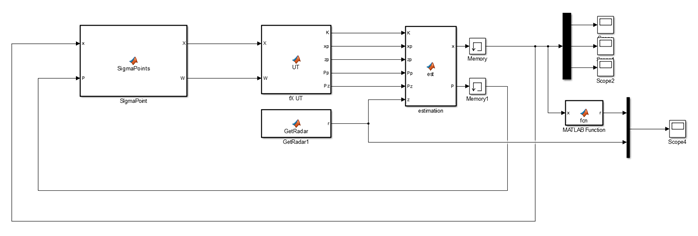

먼저 시그마 포인트를 뽑아내는 작업…chol은 cholesky decomposition
2n+1개의 시그마포인트와 weight를 계산해낸다.
이때 중요한게 x랑 P 초기값은 어디에 있느뇨….?
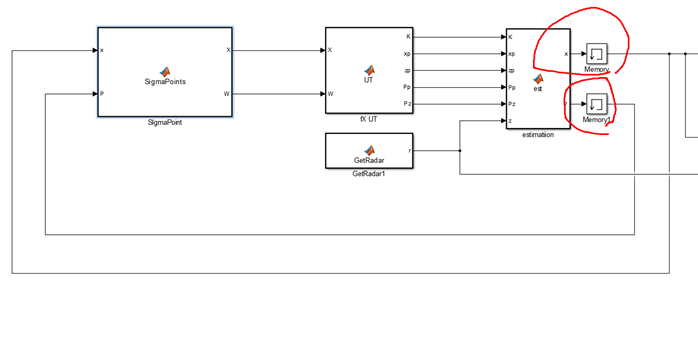
요거 메모리를 열어보면
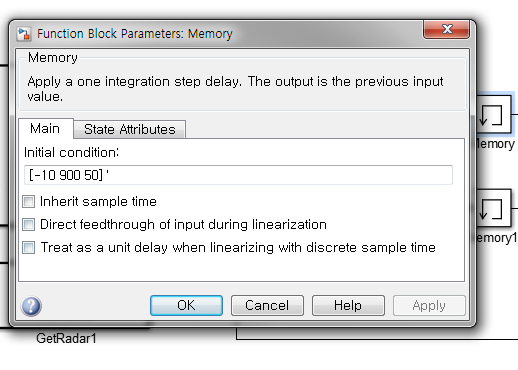
이렇게 초기값 설정 할 수 있게 해준다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 | function [K,xp,zp,Pp,Pz] = UT(X,W)
% state variable prediction dt=0.05; n=3; fX=zeros(n,2*n+1); xp=zeros(n,1); Pp=zeros(n,n); Q=0.001*eye(3);
for i=1:2*n+1 fX(:,i)=(eye(3)+[0 0 dt;0 0 0;0 0 0])*X(:,i); end
for i=1:2*n+1 xp=xp+W(i)*fX(:,i); end
for i=1:2*n+1 Pp=Pp+W(i)*(fX(:,i)-xp)*(fX(:,i)-xp)'; end Pp=Pp+Q; % measured value prediction m=1; hX=zeros(m,2*n+1); zp=zeros(m,1); Pz=zeros(m,m); R=100; for i=1:2*n+1 hX(:,i)=sqrt(X(1,i)^2+X(2,i)^2); end for i=1:2*n+1 zp=zp+W(i)*hX(:,i); end for i=1:2*n+1 Pz=Pz+W(i)*(hX(:,i)-zp)*(hX(:,i)-zp)'; end
Pz=Pz+R;
% calculate kalman gain Pxz=zeros(n,m); K=zeros(n,m);
for i=1:2*n+1 Pxz=Pxz+W(i)*(fX(:,i)-xp)*(hX(:,i)-zp)'; end K=Pxz*inv(Pz); |
그담 이제 fX랑 hX 계산해서 K,xp,zp,Pp,Pz를 계산하는 것이다.
여기서 fX는 xp계산의 후보군이 되는 포인트들이다.
hX는 zp의 후보군이 되는 포인트들인 것이다. 각각의 시그마 포인트들로 계산하는 것이다.
Px+Q랑 Pz+R 해주시고…계산하면 된다.

마지막으로 측정값을 참고하여 계산하면 된다.
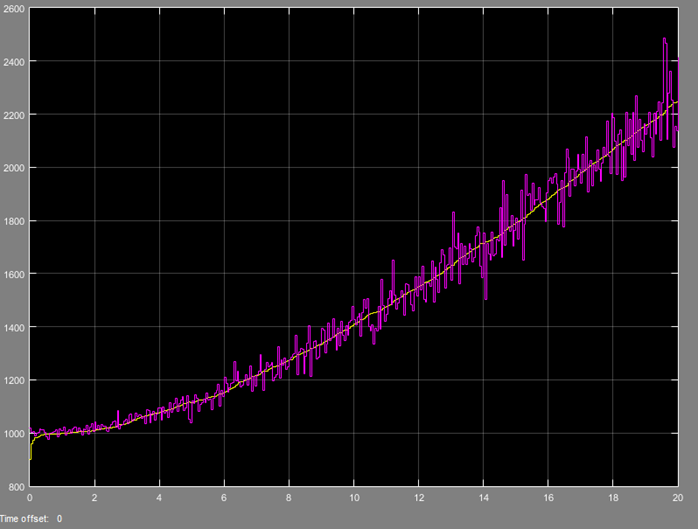
결과는 물론 아주 잘 나온다.
